베이즈 정리 기초
조건부 확률, 베이즈 정리 예제에 대한 간단한 정리
조건부 확률이란?
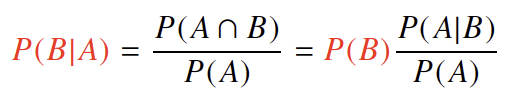
\(P(B \vert A)\) : 특정한 사건 A가 일어났을때 사건 B가 일어날 확률
베이즈 정리를 이용하면, A라는 새로운 정보가 주어졌을때 이를 사전확률로 이용하여 P(B)로부터 P(B|A)를 계산하는 방법을 제공한다.
예측의 관점에서 베이즈 정리를 이용하게 되면, 어떤 사건이 일어날 확률을 계산할 때 다른 정보가 있다면 이를 토대로 더욱 구체적으로 예측할 수 있게 된다.
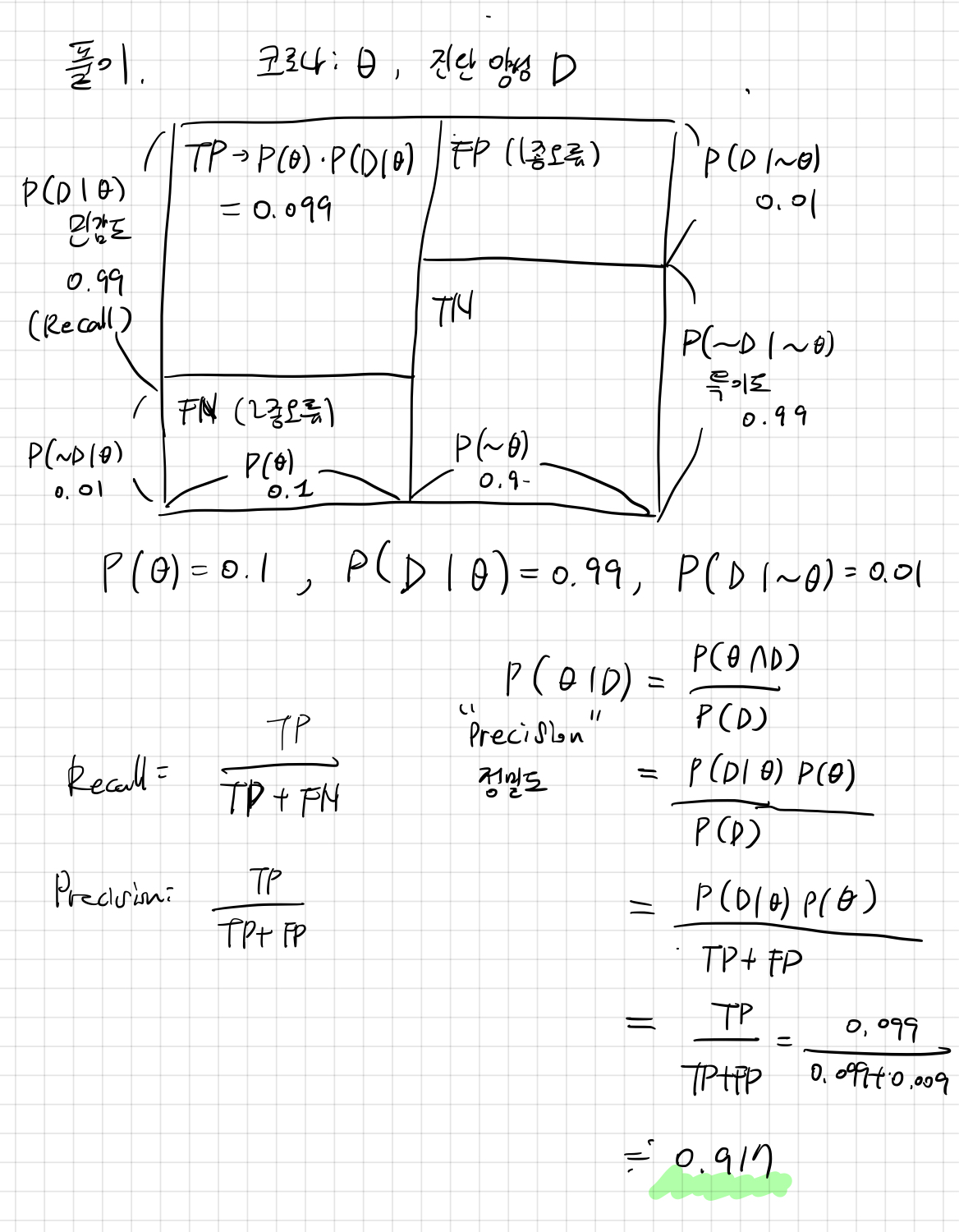
베이즈 정리 예제 - 코로나바이러스
코로나의 발병률이 10%이고, 코로나에 실제로 걸렸을 때 검진될 확률이 99%, 실제로 걸리지 않았을 때 오검진될 확률이 1%라고 했을 때, 어떤 사람이 질병에 걸렸다고 검진결과가 나왔을 때 정말로 코로나에 감염되었을 확률은?
베이즈 정리를 통한 정보의 갱신
앞서 계산한 사후확률을 사전확률로 사용하여 갱신된 사후확률을 계산할 수 있다.
앞서 검진받았던 사람이 두 번째 검진을 받았을 때도 양성이 나왔을 때 정말로 코로나에 감염되었을 확률은?

앞서 검진받은 사실을 기반으로 베이즈 정리에 기반해 확률을 갱신하면 두 번 양성이 나왔기 때문에 신뢰도는 더욱 올라가게 된다.
베이즈 정리를 통해 살펴볼 수 있는 점은 베이지안 확률론이 이전의 빈도주의적인 확률 계산과 다르다는 것이다. 처음부터 확률이 정해진 것이 아니고, 사전확률과 같은 경험에 기반하여 주어진 정보를 바탕으로 사전확률을 갱신해 나간다.
Reference.
https://angeloyeo.github.io/2020/01/09/Bayes_rule.html